doodles and coral reefs
I was doodling idly on some paper the other day, and things got a bit out of hand because trying to understand what was happening led me into the world of "Schläfli symbols" and hyperbolic geometry, and finally into crochet, coral reefs and curly kale.
Here are the instructions for this particular type of doodle:
Step 1. Let's choose n=5, the pentagon:
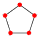
Step 2. Let's choose p=3, so we just need to draw one extra line on each corner:
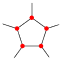
Step 3. We fill in the gaps with more pentagons:
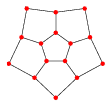
Step 2 again: We add five more lines on the outside where needed:
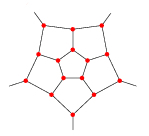
Step 3 again: We add more pentagons in the gaps. They're a bit stretched but that's ok.

Step 2 again: Oh wait, there are already 3 lines coming from each corner. We can't go any further. The doodling algorithm has come to a stop.
Hmmm... well it's kind of pretty but so what?
Let's do another one, with n=6 (hexagons). Step 1:
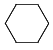
Step 2: extend one more line from each corner:
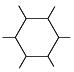
Step 3: join the lines up with more hexagons:
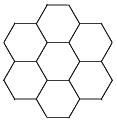
Step 2 again: more lines:
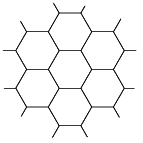
Step 3 again: more hexagons:

We're drawing a honeycomb, and can continue this for as long as we want - unlike the pentagon case this one goes on forever without ever coming to a stop.
Let's try one more, with n=7 (heptagons). Step 1:
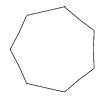
Step 2: extend a line from each corner:
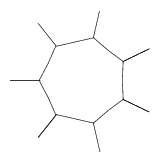
Step 3: join the lines up with heptagons:

Step 2 again: extend a line from each corner that needs one:

Step 3 again: fill in the gaps with heptagons.

Wow that's a lot of heptagons already. Let's stop there.
With n=7 and greater it quickly gets hard to draw because there are too many polygons around the outside. It's not like the n=6 case where the tiling was nice and regular. You can draw the n=7 case on a piece of paper but only by making the outer polygons get smaller and smaller, or more and more stretched. Wikipedia has a page with the same drawing here and tells us that the method of making the polygons get smaller and smaller is called the Poincaré disk model for rendering hyperbolic geometry. It also tells us that this tiling is given the Schläfli symbol {7,3} because n=7 and p=3.
Let's try one last one, with n=4 (still with p=3 lines from each corner). Step 1:

Step 2: extend lines from each corner:

Step 3: join up the lines with squares (well, squashed squares):

Step 2 again: nothing to do, every corner already has 3 lines coming out.
There's something familiar about this image - it looks like a cube. And now when you think about it the finished n=5 image at the top looks like a flattened dodecahedron. Those two doodles ended up by closing in on themselves (much like the way clathrin does when it assembles itself). But for n=6 you get a flat plane, while the n=7 graph gets all jammed up at the edges. There's something very odd going on.
Let's make a table of what happens for different values of n and p:
All five platonic solids appear in this table like magic. All three regular tilings of the plane appear too. The rest of the table is all hyperbolic.
(This table isn't my discovery, by the way, it's just the table of Schläfli symbols for regular polygons. But I've never seen it written out in full like this.)
(There's also an interesting symmetry in the table above. Take any two entries that are positioned symmetrically across the diagonal, like {5,3} and {3,5}, the dodecahedron and icosahedron. These shapes/tilings are duals of each other. Entries along the diagonal are self-dual.)
So what is this hyperbolic geometry? It's actually more familiar than you might think. Lettuce is a good example:
 (source)
(source)
You can take any part of a lettuce leaf and flatten it down, but you can't flatten the whole thing without folding or tearing it. Curly kale is more extreme:
 (source)
(source)
It gets more and more frilled as you move away from the stalk, just like our heptagons got more and more jammed in. It's closely related to the fractal branching of trees, except that the branches stay joined together by flaps of skin. The veins on a lettuce leaf show this very clearly.
You can make your own hyperbolic geometry by cutting out lots of heptagons from paper and sellotaping them together. The resulting sheet will leap off the table into a frilled form exactly like lettuce. (Instructions and a printable template here.)
Daina Taimina realised that a better way to make these hyperbolic forms is to crochet them:
 (source)
(source)
Since then Margaret Wertheim and others have been crotchet-ing like crazy, making knitted coral reefs to both draw attention to global warming and demonstrate hyperbolic geometry:
 (source)
(source)
Her TED talk on the subject is well worth watching, even if none of the mathematics interests you.
Here are the instructions for this particular type of doodle:
1. Draw an n-sided figure. 2. From each corner, extend out more lines until there are p in total coming from that corner. 3. Fill in the gaps between the lines with more n-sided polygons. 4. Repeat from step 2. |
Step 1. Let's choose n=5, the pentagon:

Step 2. Let's choose p=3, so we just need to draw one extra line on each corner:

Step 3. We fill in the gaps with more pentagons:

Step 2 again: We add five more lines on the outside where needed:

Step 3 again: We add more pentagons in the gaps. They're a bit stretched but that's ok.

Step 2 again: Oh wait, there are already 3 lines coming from each corner. We can't go any further. The doodling algorithm has come to a stop.
Hmmm... well it's kind of pretty but so what?
Let's do another one, with n=6 (hexagons). Step 1:

Step 2: extend one more line from each corner:

Step 3: join the lines up with more hexagons:

Step 2 again: more lines:

Step 3 again: more hexagons:

We're drawing a honeycomb, and can continue this for as long as we want - unlike the pentagon case this one goes on forever without ever coming to a stop.
Let's try one more, with n=7 (heptagons). Step 1:

Step 2: extend a line from each corner:

Step 3: join the lines up with heptagons:

Step 2 again: extend a line from each corner that needs one:

Step 3 again: fill in the gaps with heptagons.

Wow that's a lot of heptagons already. Let's stop there.
With n=7 and greater it quickly gets hard to draw because there are too many polygons around the outside. It's not like the n=6 case where the tiling was nice and regular. You can draw the n=7 case on a piece of paper but only by making the outer polygons get smaller and smaller, or more and more stretched. Wikipedia has a page with the same drawing here and tells us that the method of making the polygons get smaller and smaller is called the Poincaré disk model for rendering hyperbolic geometry. It also tells us that this tiling is given the Schläfli symbol {7,3} because n=7 and p=3.
Let's try one last one, with n=4 (still with p=3 lines from each corner). Step 1:

Step 2: extend lines from each corner:

Step 3: join up the lines with squares (well, squashed squares):

Step 2 again: nothing to do, every corner already has 3 lines coming out.
There's something familiar about this image - it looks like a cube. And now when you think about it the finished n=5 image at the top looks like a flattened dodecahedron. Those two doodles ended up by closing in on themselves (much like the way clathrin does when it assembles itself). But for n=6 you get a flat plane, while the n=7 graph gets all jammed up at the edges. There's something very odd going on.
Let's make a table of what happens for different values of n and p:
| p (number of lines coming from each point) | n (number of sides on each polygon) | ||||
|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | |
| 3 | tetrahedron | cube | dodecahedron | plane | hyperbolic |
| 4 | octohedron | plane | hyperbolic | hyperbolic | hyperbolic |
| 5 | icosahedron | hyperbolic | hyperbolic | hyperbolic | hyperbolic |
| 6 | plane | hyperbolic | hyperbolic | hyperbolic | hyperbolic |
| 7 | hyperbolic | hyperbolic | hyperbolic | hyperbolic | hyperbolic |
All five platonic solids appear in this table like magic. All three regular tilings of the plane appear too. The rest of the table is all hyperbolic.
(This table isn't my discovery, by the way, it's just the table of Schläfli symbols for regular polygons. But I've never seen it written out in full like this.)
(There's also an interesting symmetry in the table above. Take any two entries that are positioned symmetrically across the diagonal, like {5,3} and {3,5}, the dodecahedron and icosahedron. These shapes/tilings are duals of each other. Entries along the diagonal are self-dual.)
So what is this hyperbolic geometry? It's actually more familiar than you might think. Lettuce is a good example:
 (source)
(source) You can take any part of a lettuce leaf and flatten it down, but you can't flatten the whole thing without folding or tearing it. Curly kale is more extreme:
 (source)
(source)It gets more and more frilled as you move away from the stalk, just like our heptagons got more and more jammed in. It's closely related to the fractal branching of trees, except that the branches stay joined together by flaps of skin. The veins on a lettuce leaf show this very clearly.
You can make your own hyperbolic geometry by cutting out lots of heptagons from paper and sellotaping them together. The resulting sheet will leap off the table into a frilled form exactly like lettuce. (Instructions and a printable template here.)
Daina Taimina realised that a better way to make these hyperbolic forms is to crochet them:
 (source)
(source)Since then Margaret Wertheim and others have been crotchet-ing like crazy, making knitted coral reefs to both draw attention to global warming and demonstrate hyperbolic geometry:
 (source)
(source)Her TED talk on the subject is well worth watching, even if none of the mathematics interests you.
This post was originally on LiveJournal.