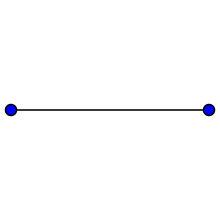
A digon is one of the regular polygons_
A digon is one of the regular polygons that you might not have encountered. It has two edges and two vertices. In Euclidean space it is degenerate (it has zero area) but in spherical space it makes perfect sense - if the vertices are antipodal.
Likewise a dihedron is (sort of) the sixth platonic solid. It is a regular polyhedron with just two faces (with any number of sides). In Euclidean space it is degenerate (has zero volume) but makes sense in a three-dimensional spherical space.
Likewise a dihedron is (sort of) the sixth platonic solid. It is a regular polyhedron with just two faces (with any number of sides). In Euclidean space it is degenerate (has zero volume) but makes sense in a three-dimensional spherical space.
Digon - Wikipedia, the free encyclopedia
Shared with: Public
Dave Wonnacott - 2011-11-24 12:26:17+0000
Hmmm... So if I drew on a sphere a 'wedge' whose sides weren't great circles (vertices non antipodal), would that be a digon? Presumably not, but what would it be?
Tim Hutton - 2011-11-24 12:32:03+0000
I think: Those sides wouldn't be straight lines - only great circles are straight lines in a spherical space.
Dave Wonnacott - 2011-11-24 13:02:19+0000
I guessed that might be the case, but that's a matter of definition then, isn't it? A digon is only a digon if and only if it's composed of "shortest distance" edges. I was wondering what was the difference between a digon defined that way, and any other way. Maybe it's because (he says, thinking about it a bit harder) because the wedge I originally defined isn't degenerate in Euclidean space? It's the degeneracy that defines the digon? (How onomatopoeic...)
Tim Hutton - 2011-11-24 13:23:48+0000
We could define 'curvagons' to be polygons with curved edges, like the Reuleaux triangle. A regular curvagon would have n identical curved segments joined in a circle.
This post was originally on Google+
