_You, James Clerk Maxwell, know in 1865
"You, James Clerk Maxwell, know in 1865 from the work of Isaac Newton and others that light is made of some sort of waves. But nobody in the world knows what sort of waves they are. Nobody knows what light actually is.
You stop.
Nobody in the world - except you - knows what light actually is.
You realise that you are the first person in all of history to know what light is made of. Can you imagine that feeling?
Light is electric and magnetic fields, wriggling through space together."
You stop.
Nobody in the world - except you - knows what light actually is.
You realise that you are the first person in all of history to know what light is made of. Can you imagine that feeling?
Light is electric and magnetic fields, wriggling through space together."
Originally shared by Cliff HarveyYesterday was James Maxwell's birthday (13 June 1831 – 5 November 1879) today. (thanks +Cytia Beata )
So here inside the link are the famous Maxwell's equations explained in a relatively simple way.
Maxwell's equations are sublimely beautiful, but I especially think they're good for illustrating the main trend in physics knowledge: As you move to progressively more fundamental, natural levels of description, what initially looks looks like a mess can be expressed more and more compactly based on fewer and fewer independent ideas.
One of the first ways this happens is through the concept of a vector. Its really strange to think how back in the day, these things had to be written out as 8 equations of just numbers. But by writing the variables in terms of vectors (in boldface) we get a dramatic simplification. What's not fully obvious when learning the machinery of vectors is why that simplification is achieved. It comes down to symmetry: a vector isn't just any collection of numbers but something that must be interpretable as an "arrow" in space. To be consistent with this idea, a vector must transform in the correct way under rotations. And the laws of physics shouldn't depend on any choice of orientation. This just boils down to the fact that space has no predefined coordinate axes. It takes some thought to fully appreciate how the simplification of this language is related to the denial of the concept of a physical coordinate system. This is also why its possible to explain what Maxwell's equations say in words; people intuitively know how to deal with things that have to make sense "in space".
Even when Maxwell's equations are written in terms of vectors, its still pretty obvious just looking at them that there is more implicit structure there that is not yet fully captured. Explicating that structure lead to the discovery of special relativity, and this relativity brings a new simplification: The two vector fields are actually components of a single tensor (a matrix) that must transform into each other. This new choice of variables is quickly summarized in this image, and you can see the dramatic simplicity at the bottom line: http://i.imgur.com/rOucK.jpg
So by jettisoning extraneous concepts the number of equations is reduced from 8 to 4 to 2.
Of course, its also tough not to notice that those last two equations expressing the content of Maxwell's equations also have a pretty obvious relationship between them: they are symmetrical under the exchange of E and B fields and electric charges with magnetic charges. And that observation actually brings you into contact with some very high falutin concepts in quantum gravity: S-duality, black holes, holography and so on...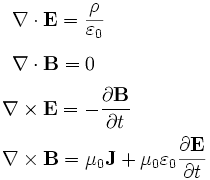
So here inside the link are the famous Maxwell's equations explained in a relatively simple way.
Maxwell's equations are sublimely beautiful, but I especially think they're good for illustrating the main trend in physics knowledge: As you move to progressively more fundamental, natural levels of description, what initially looks looks like a mess can be expressed more and more compactly based on fewer and fewer independent ideas.
One of the first ways this happens is through the concept of a vector. Its really strange to think how back in the day, these things had to be written out as 8 equations of just numbers. But by writing the variables in terms of vectors (in boldface) we get a dramatic simplification. What's not fully obvious when learning the machinery of vectors is why that simplification is achieved. It comes down to symmetry: a vector isn't just any collection of numbers but something that must be interpretable as an "arrow" in space. To be consistent with this idea, a vector must transform in the correct way under rotations. And the laws of physics shouldn't depend on any choice of orientation. This just boils down to the fact that space has no predefined coordinate axes. It takes some thought to fully appreciate how the simplification of this language is related to the denial of the concept of a physical coordinate system. This is also why its possible to explain what Maxwell's equations say in words; people intuitively know how to deal with things that have to make sense "in space".
Even when Maxwell's equations are written in terms of vectors, its still pretty obvious just looking at them that there is more implicit structure there that is not yet fully captured. Explicating that structure lead to the discovery of special relativity, and this relativity brings a new simplification: The two vector fields are actually components of a single tensor (a matrix) that must transform into each other. This new choice of variables is quickly summarized in this image, and you can see the dramatic simplicity at the bottom line: http://i.imgur.com/rOucK.jpg
So by jettisoning extraneous concepts the number of equations is reduced from 8 to 4 to 2.
Of course, its also tough not to notice that those last two equations expressing the content of Maxwell's equations also have a pretty obvious relationship between them: they are symmetrical under the exchange of E and B fields and electric charges with magnetic charges. And that observation actually brings you into contact with some very high falutin concepts in quantum gravity: S-duality, black holes, holography and so on...
Irregular Webcomic! #1420
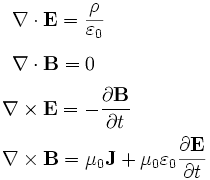
Shared with: Public
+1'd by: Felix Woitzel
This post was originally on Google+
