The Wallis Sieve is a variant on the Si

Tim Hutton - 2016-11-09 14:00:34+0000 - Updated: 2016-11-09 14:01:52+0000

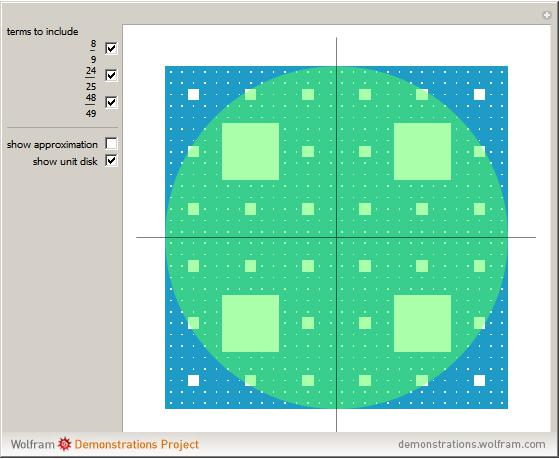
The Wallis Sieve is a variant on the Sierpiński Carpet. It has the remarkable property that the remaining area (in blue) is equal to the unit circle, shown in green.

Blog post about it by +Ed Pegg:
http://community.wolfram.com/groups/-/m/t/822984

We're hosting a workshop to learn about the work of John Wallis. If you're in Cambridge, UK on Sunday 27th November then come along:
http://www.cambridgelovelace.org/

The Wallis Sieve is a variant on the Sierpiński Carpet. It has the remarkable property that the remaining area (in blue) is equal to the unit circle, shown in green. Blog post about it by +Ed Pegg: http://community.wolfram.com/groups/-/m/t/822984 We're hosting a workshop to learn about the work of John Wallis. If you're in Cambridge, UK on Sunday 27th November then come along: http://www.cambridgelovelace.org/

Shared with: Public, Ed Pegg, Evelyn Lamb

+1'd by: Math Solver, Gitesh Khodiyar, Don Whitaker, Roice Nelson, David Eppstein, Rubén Perblac, Dmitry Shintyakov

Tim Hutton - 2016-11-09 14:20:03+0000

Another blog post about it, by +Evelyn Lamb: https://blogs.scientificamerican.com/roots-of-unity/a-few-of-my-favorite-spaces-the-wallis-sieve/

A Few of My Favorite Spaces: The Wallis Sieve

Tim Hutton - 2016-11-10 14:21:58+0000

+Evelyn Lamb's attempts to find a visual explanation for why the Wallis Sieve gives the area of a circle are intriguing. +Ed Pegg mentions the connection to Farey sequences and has a picture of Ford circles. I want to believe that somehow we can marshal the square holes to make a pattern like Ford circles and thus obtain a circle in the limit.
https://en.wikipedia.org/wiki/Ford_circle

Ford circle - Wikipedia

This post was originally on Google+